4 - (1). 수식 트리 만들기 ( 수식 트리 구성 & 수식 트리 계산 )

이진 트리 순회는 수식 트리를 처리하는데 사용될 수 있다.

수식 트리는 산술식이나, 논리식의 연산자와 피연산자들로부터 만들어진다.

피연산자들은 단말 노드가 되며, 연산자는 비단말 노드가 된다.

각 이진 연산자에 대하여 왼쪽 서브 트리는 왼쪽 피연산자가 되며,

오른쪽 서브 트리는 오른쪽 피연산자를 나타낸다.

[ 그림1 ]

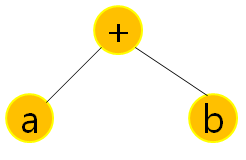
[ 그림2 ]

[ 그림3 ]

구성에 앞서, 수식 트리 구성하는 함수와 수식 트리 계산하는 함수는

ExpressionTree 헤더 파일과 ExpressionTree 소스 파일에 정의.

 

1. 수식 트리 구성하기

수식 트리를 구성하기에 앞서 수식은 후위 표기법의 수식이며, 만약 중위 표기법의 식이면

이를 후위 표기법으로 변경이 필요하다.

아래의 글을 읽어보자.

designatedroom87.tistory.com/23?category=868809

스택의 활용 - 중위 표기법에서 후위 표기법으로 변환(괄호 제외)

그리고 앞에서 만든 스택을 활용하는데, 저장할 데이터가 이진 트리의 노드이므로 이에 약간의 수정이 필요.

수식 트리의 구성 작업 순서는 아래와 같다.

      (1). 후위 수식 배열을 탐색을 하면서, '숫자(피 연산자)' 이면 스택에 저장.

      (2). 만약, '연산자' 이면, 스택에서 노드 2개를 뽑아서 '연산자'의 자식으로 연결하고 다시 스택에 저장.

      (3). 이와 같은 작업을 반복하면, 스택에 노드는 하나만 남는데, 이는 곧 수식 트리의 루트이다.

 

수식 트리를 구성하는 함수는 아래와 같다.

 

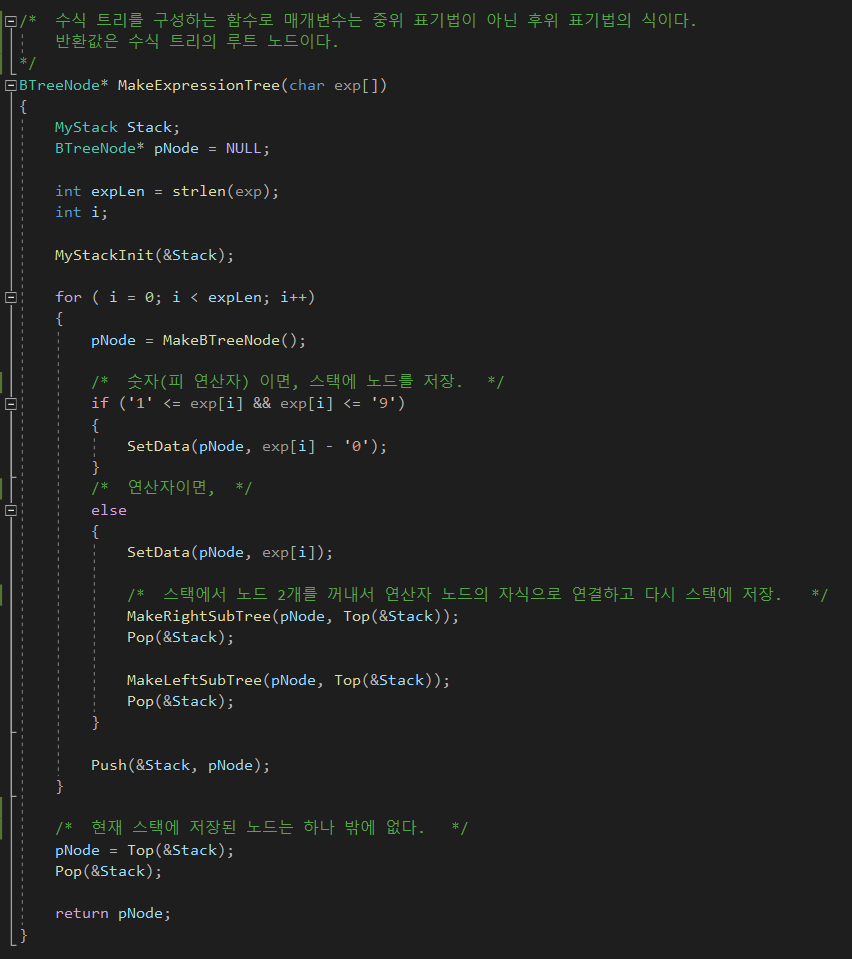
2. 수식 트리 계산하기

수식 트리의 루트 노드는 연산자이다.

따라서 이 연산자의 피연산자인 서브 트리들만 계산되면 전체 수식을 계산할 수 있다.

각 각의 서브 트리에서도 마찬가지로 자식 노드만 계산되면

루트에 저장된 연산자를 이용하여 수식을 계산할 수 있다.

따라서, 여러가지 순회 방법 중에서 가장 적합한 순회방식은 자식 노드를 먼저 방문하는

후위 순회라 할 수 있을 것이다.

후위 순회는 항상 자식 노드들을 먼저 방문한 다음에, 루트 노드를 방문하기 때문이다.

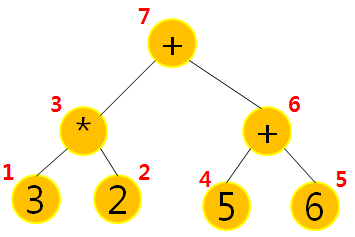
[ 그림 4 : 수식 트리 ]

 

수식 트리 계산 알고리즘 의사코드

위의 알고리즘을 설명하면,

두 번째 if문의 의미는 만약 자식 노드들이 없으면 데이터 필드 값을 반환한다.

5번째 문장은 왼쪽 서브 트리에 대하여 evaluate를 재귀 호출한다.

6번째 문장은 오른쪽 서브 트리에 대하여 evaluate를 재귀 호출한다.

7번째 문장은 데이터 필드에서 연산자를 추출한다.

8번째 문장은 추출한 연산자를 가지고 연산을 수행해서 결과값을 반환한다.

 

수식 트리를 계산하는 함수는 아래와 같다.

 

아래는 메인 함수

 

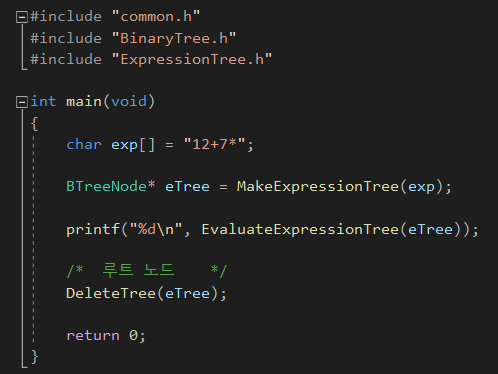
아래는 프로그램 실행결과

 

기존의 DeleteTree 함수에서 약간의 변경을 했다.

그 이유는 노드에 들어간 데이터는 숫자와 연산자인데, 숫자 노드면 숫자를 출력하고

연산자 노드면 단일문자로 출력하도록 변경했다.

아래와 같다.

 

헤더 파일 & 소스 파일

BinaryTree.c

0.00MB

BinaryTree.h

0.00MB

common.h

0.00MB

ExpressionTree.c

0.00MB

ExpressionTree.h

0.00MB

main.c

0.00MB

MyStack.c

0.00MB

MyStack.h

0.00MB