조약돌 놓기 문제

문제 출처

<쉽게 배우는 알고리즘 내용 >

 

문제

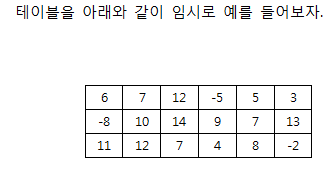
i열에 돌을 둘 수 있는 가지수를 살펴보자.

위의 임시 테이블에 i열을 다음과 같이 설정하자.

 

i열에 돌을 둘수 있는 경우의 수를 파악하자.

아래와 같이 4가지 경우가 있음을 알 수 있다.

<Pattern 1>

<Pattern 2>

<Pattern 3>

<Pattern 4>

i열에 돌을 둘 수 있는 가지수는 4가지임을 알 수 있다.

우선 최적 부분구조의 존재를 확인해보자.

n열 중 1열부터 i열까지 돌을 놓는 경우에 1열부터 i열까지의 합의 최고치를 생각해보자.

위에서처럼 i열에는 4가지 패턴 중 하나의 경우로 돌이 놓여질 것이다.

 

(1). i열이 패턴1로 놓여 있을 경우의 최고점

(2). i열이 패턴2로 놓여 있을 경우의 최고점

(3). i열이 패턴3으로 놓여 있을 경우의 최고점

(4). i열이 패턴4로 놓여 있을 경우의 최고점

 

그리고, 다음과 같은 경우에 대해서도 생각을 해야한다.

i열이 패턴4로 놓여있으면 i-1열은 반드시 패턴2로 놓여야 한다.

따라서, i열이 패턴4로 놓여 있을 경우의 최고점은

i-1열이 패턴2로 놓여 있을 경우의 최고점과 i열에서 패턴4로 돌이 놓인 곳에 있는 수를 합한 점수이다.

그리고, i열이 패턴1로 놓여 있을 경우의 최고점은

i-1열이 패턴2로 놓여 있을 최고점과 i-1열이 패턴3으로 놓여 있을 경우의 최고점 중 큰 것과

i열에서 패턴1로 돌이 놓은 곳에 있는 수를 합한 점수이다.

이처럼 i열까지의 최적해는 i-1열까지의 최적해를 포함하고 있다.

즉, 자신보다 크기가 하나 작은 문제의 최적해를 자신의 최적해를 구성하는데에 사용한다.

최적 부분구조를 가지고 있는 것이다.

 

최적 부분구조를 정리해보자.

M은 최대값을 반환하는 함수이다.

이제 밑에서 이 최적 부분구조를 가진 문제를 재귀적으로 구현해보자.

 

알고리즘 의사코드

위의 알고리즘은 Pebble( n,1 ) ~ Pebble( n,4 )의 결과 중 최대값이 답이다.

 

구현 방식

재귀 함수를 통해 구현할 것이다.

아래의 그림을 보자. 문제를 좁히기 위해 열의 개수는 개로 고정을 해보자.

 

아래의 그림은 위의 그림을 좀 더 자세히 기술한 것이다.

아래의 그림을 요약하면 맨 마지막 열의 위치에 돌을 패턴1로 둔 상태에서 그 때의 최고점을 구하는

과정을 나타낸 것이다.

여러 점수들 중에서 가장 높은 점수를 찾으면 된다. 

 

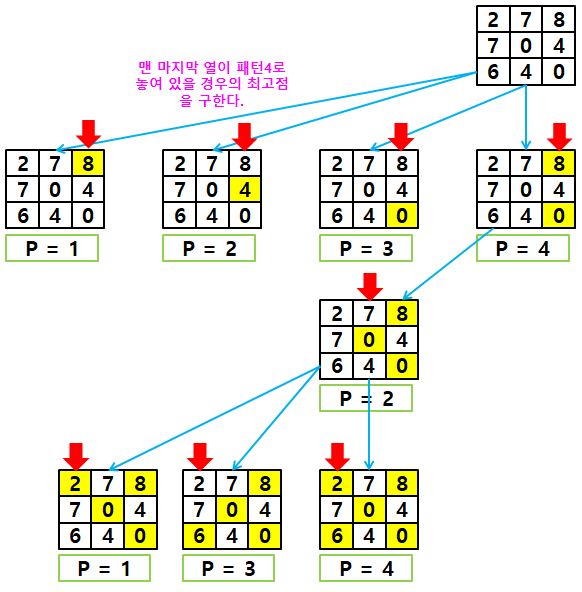
아래의 그림은 맨 마지막 열의 위치에 돌을 패턴2로 둔 상태에서 그 때의 최고점을 구하는

과정을 나타낸 것이다.

여러 점수들 중에서 가장 높은 점수를 찾으면 된다.

 

아래의 그림은 맨 마지막 열의 위치에 돌을 패턴3으로 둔 상태에서 그 때의 최고점을 구하는

과정을 나타낸 것이다.

여러 점수들 중에서 가장 높은 점수를 찾으면 된다.

 

아래의 그림은 맨 마지막 열의 위치에 돌을 패턴4로 둔 상태에서 그 때의 최고점을 구하는

과정을 나타낸 것이다.

여러 점수들 중에서 가장 높은 점수를 찾으면 된다.

 

구현

프로그램 실행결과

 

소스 파일

main.c

0.00MB

 

동적 프로그래밍

위에서, Pebble함수가 중복호출이 되고 있다.

위의 문제의 최적 부분구조와 재귀적 구현에서의 중복 호출을 확인하였다.

이로부터 이 문제가 동적 프로그래밍의 좋은 대상이 됨을 알 수 있다.

 

이 문제에 존재하는 부분 문제를 모두 나열하면

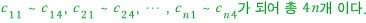
함수 Pebble을 한 번 호출하는 것은 부분 문제 한 개와 대응한다.

이 4n개를 아래에서부터( 작은 것부터 ) 저장해 가면서 구하면 된다.

아래는 의사코드이다.

부분 문제들의 답을 n X 4 배열 peb[][]에 저장한다.

 

동적 프로그래밍 구현

아래는 저장하기 위한 배열

아래의 함수는 돌을 둔 최고점을 구하는 함수이다.

아래는 메인 함수 부분.

프로그램 실행결과

 

소스 파일

main.c

0.00MB