API를 활용한 이차함수를 이용해 점프 기능 만들기

 

a가 양수냐, 음수냐에 따라서 이차함수의 그래프의 개형이 달라진다.

그림 출처 : terms.naver.com/entry.nhn?docId=945470&cid=47324&categoryId=47324

이차함수의 그래프

 

글의 제목에서 말했듯이 이차함수를 게임에서 접목하는 부분은 점프를 만드는데 활용할 수 있다.

위의 식보다는 간편하게 위와 같이 쓰도록 하자.

위 식의 그래프를 그려보면, 아래와 같다.

보통 x축은 시간으로 표기한다. y축은 점프의 높이.

그리고, 시간은 0에서부터 시작 한다.

그래프를 해석하면,

0에서 점프의 높이는 0이며, 시간이 지남에 따라서

점프의 높이가 서서히 증가하다가, 점프의 최대높이에 다다르면

점프의 높이가 서서히 줄어들어서, a시간이 되면 높이가 0이므로

이 때, a시간에서 점프가 끝나는 시점이 된다.

그리고, 좀 더 그래프를 심오하게 그려보자.

위의 그래프는 첫 번째 그림의 그래프를 크게 확대한 것으로,

빨간색 선이 보일 것이다.

위의 구간을 시간 0에서 점프최대높이일때의 시간까지만 고려해보자.

그러면, 시간이 0에서 빨간색 선의 기울어짐이 가파르다가 시간의 흐름에 따라서

빨간색 선의 기울어짐이 서서히 완만해짐을 보이다가

점프최대높이 일때, 기울어짐이 없어졌다.

즉, 이부분을 놓고 다음과 같이 해석할 수 있다.

점프를 할 시에 급격하게 올라가다가 서서히 올라간다.

그러다가 점프최대높이일 때의 시간을 지나게 되면, 천천히 하락하다가

빠르게 하락한다.

 

점프 함수의 구현

우선 변수부터 선언을 하는데, 모두 전역 변수들이다.

구현의 방식은 공을 하나 만들어서 스페이스 바가 눌리면 공이 점프했다가 착지하는 것이다.

그리고 API는 좌측상단이 원점이고 오른쪽으로 갈수록 x좌표가 커지고 아래로 갈수록 y좌표가 커진다.

변수들에 대한 간략한 설명은 아래에서 한다.

구현함 함수는 아래의 세 함수들이다.

아래의 Jump함수에서 식의 부호가 다름을 알 수 있는데, 이와 같이 적은 이유는

API의 좌표계가 우리가 수학에서 쓰는 좌표계와 다르기 때문이다.

즉, 점프 시에 y값이 작아져야 위로 올라가고 y값이 커져야 아래로 내려온다.

즉, 최대점프시간에 JumpHeight값이 가장 작은 음수가 된다. 기존의 y좌표값에 이 값을 더하면 

y좌표값은 가장 작은 값이 되므로 가장 높이 올라간 위치가 된다. 

음수식을 적용하고 Draw함수의 y좌표의 렌더할 위치를 뺄셈으로 바꾸면 된다.

 

JumpHeight는 공이 현재 위치에서의 점프높이를 의미하는 변수.

JumpTime은 x축. 시간을 나타냄.

jumpPower는 상수a값. 우리가 임의로 조정할수 있다.

 

if의 조건은 쉽게 생각하면, 시간이 a값을 넘어가면 착지를 한 경우이므로

변수들을 초기화 시켜주는 과정이다. 점프후에 착지한 과정이기 때문에 점프의 높이를 0으로 초기화 함.

 

프로그램 실행결과

 

소스 파일

Jump.cpp

0.00MB

 

다이나믹한 점프 구현

이번 다이나믹점프구현에서는 위의 이차방정식을 그대로 사용을 할 것이다.

다만 일반적인 점프하고 다른 점은, y축이 점프의 높이가 아닌 점프의 속도로 이용할 것이다.

그러면, 점프의 높이는 어떻게 구하느냐가 문제일 것이다.

그 부분은 바로 적분을 이용해서 구한다.

위의 그래프는 시간과 속도 그래프 y축은 점프의 속도이다.

즉, 위의 그래프에서 x축이 [0, a]구간까지는 점프를 해서 올라간 높이( 점프한 높이 )이며,

[a,k]구간은 점프를 하고나서 아래로 내려오는 구간이다.

즉, x = k 에서 점프가 끝나고 바닥에 착지한 시간임을 알 수 있다.

앞 장에서, a값은 상수값으로 우리가 원하는 임의의 값을 지정해줄수 있다고 하였다.

그러면, 여기에서 문제점은 k값은 우리가 모르는 값이 된다. k값을 구하는 과정이 필요하다.

그리고, 두 면적( 혹은 넓이 )이 같다고 가정하면, k값을 구할 수 있다.

즉, 정적분의 개념을 이용하면,

S1 + S2 = 0  이 된다.

아래에서 k값을 구하고, 프로그램 코딩상에서 어떻게 작성할지 보도록 하자.

F(x)를 이용해서 S1과 S2를 아래와 같이 정리 할 수 있다.

F(k)와 F(0)을 구해보자.

그리고, 이를 위의 식에 대입하자.

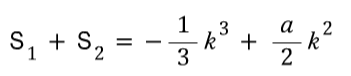
S1 + S2 = 0 이라고 하였으므로

아래와 같이 정리가 된다.

k값을 손으로 굳이 계산할 필요가 있겠냐는 생각이 있지만,

손으로 직접 계산을 하는 이유는

프로그램 상으로 위의 k값을 구하는 식을 코딩하기가

상당히 어렵기 때문에, 직접적으로 k값을 구한 것이다.

k값의 용도는 점프를 하고 나서 착지한 시간이다. 

a값은 우리가 지정할 상수이므로, 이에 따라 k값은 바로 결정이 된다.

구현에 앞서 필요한 변수들을 알아보자.

아래는 모두 전역 변수들이다.

위의 방식과 다른 점이 변수 k가 추가되었다는 것이다.

그것 말고는 없다.

점프구현 함수를 보자.

위 함수의 JumpHeight를 구하는 부분을 다시 보자.

위의 식에서 시간 구간 [0,k]를 k등분을 한 후에 면적의 누적합이 곧, 점프 높이로 구한 것이다.

마지막에 0.03을 곱한 이유는 0.03을 곱하지 않으면 너무 높이 뛴다. 그래서 보간한 값이다.

속도의 면적이 곧 높이(혹은 넓이) 이다.

 

프로그램 실행결과

 

소스 파일

Jump.cpp

0.00MB

 

별도로 만일 점프 기능을 위와 같이 구현하지 않고 아래와 같이 구현할 수도 있다.

 

프로그램 실행결과

 

소스 파일

Jump.cpp

0.00MB