Quick Sort

퀵 정렬도 분할 정복 방법에 근거한다.

여기서 정렬방식은 오름차순 기준이다.

퀵 정렬은 합병 정렬과 비슷하게 전체 리스트를 2개의 부분 리스트로 분할하고,

각 각의 부분 리스트를 다시 퀵 정렬하는 전형적인 분할 정복 방법을 사용한다.

그러나, 병합 정렬과는 달리 퀵 정렬은 리스트를 다음과 같은 방법에 의해 비 균등하게 분할한다.

먼저, 리스트 안에 있는 한 요소를 피봇으로 선택한다.

여기서는 리스트의 첫 번째 요소를 피봇으로 하기로 한다.

피봇보다 작은 요소들은 모두 피봇의 왼쪽으로 옮겨지고 피봇보다 큰 요소들은

모두 피봇의 오른쪽으로 옮겨진다.

결과적으로 피봇을 중심으로 왼쪽은 피봇보다 작은 요소들로 구성되고,

오른쪽은 피봇보다 큰 요소들로 구성된다.

이 상태에서 피봇을 제외한 왼쪽 리스트와 오른쪽 리스트를

다시 정렬하게 되면 전체 리스트가 정렬한다.

 

[그림 1 : 퀵 정렬은 피봇을 기준으로 두 개의 리스트로 나눈다.]

퀵 정렬에서 가장 중요한 함수가 Partition함수가 된다.

Partition함수의 역할이 위의 역할이다.

Partition함수는 데이터가 들어있는 배열 list의 left부터 right까지의 리스트를,

피봇을 기준으로 2개의 부분 리스트로 나누게 된다.

피봇보다 작은 데이터는 모두 왼쪽 부분 리스트로, 큰 데이터는 모두 오른쪽 부분 리스트로 옮겨진다.

 

 

이를 위하여 [그림 2]의 {5,3,8,4,9,1,6,2,7} 리스트를 두 개의 부분 리스트로 나누는 과정을 자세히 살펴보자.

먼저, 간단히 하기 위하여 피봇값을 입력 리스트의 첫 번째 데이터로 하자.

따라서, 이 경우에 피봇값은 5가 된다.

2개의 인덱스 변수 low와 high를 이용하도록 하자.

low는 왼쪽 부분 리스트를 만드는데 사용되고, high는 오른쪽 부분 리스트를 만드는데 사용된다.

인덱스 변수 low는 왼쪽에서 오른쪽으로 탐색해가다가 피봇 보다 큰 데이터(8)를 찾으면 멈춘다.

인덱스 변수 high는 오른쪽 끝에서부터 왼쪽으로 탐색해가다가 피봇보다 작은 데이터(2)를 찾으면 멈춘다.

탐색이 멈춰진 위치는 각 부분 리스트에 적합하지 않은 데이터이다.

따라서, low와 high가 가리키는 두 데이터를 서로 교환한다.

이러한 탐색-교환 과정은 low와 high가 엇갈려 지나지 않는 한 계속 반복한다.

알고리즘이 진행되면서 언젠가는 low와 high가 엇갈려서 지나가게 되면서 멈추게 한다.

이 때, high가 가리키는 데이터(1)와 피봇(5)을 교환하게 되면, 피봇을 중심으로 왼쪽 리스트에는

피봇보다 작은 데이터만 존재하게 되고, 오른쪽 리스트에는 피봇보다 큰 데이터만 존재하게 된다.

정리하면,

low와 high를 왼쪽과 오른쪽에서 출발시켜서 부적절한 데이터를 만나게 되면 교환하고

아니면 계속 진행하다가 서로 엇갈리게 되면 멈춰서 피봇을 중앙으로 이동시키게 되면

피봇을 기준으로 2개의 리스트로 나누어지게 된다.  

 

[그림 2 : 퀵 정렬에서 피봇을 기준으로 두 개의 리스트로 나누는 과정]

[그림 2]의 마지막 상태는 피봇(5)을 기준으로 왼쪽 리스트는 피봇보다 작은 데이터로

구성되고 오른쪽 리스트는 피봇보다 큰 데이터들로 구성되어 리스트가 분할된 것을 보여준다.

이 상태에서 피봇(5)은 전체 리스트가 정렬될 상태에서 이미 제 위치에 있음을 알 수 있다.

따라서, 피봇을 제외한 왼쪽리스트{1,3,2,4}를 독립적으로 다시 퀵 정렬하고,

또한 오른쪽 리스트{9,6,8,7}을 다시 퀵 정렬한다면 [그림 3]과 같이 전체 리스트가 정렬된다.

여기에서 녹색으로 표시된 숫자는 피봇을 나타낸다.

 

[그림 3 : 퀵 정렬의 전체과정]

위의 [그림 3]은 재귀함수의 호출 스택과 같다.

1. [0,8] 범위의 인덱스를 기준으로 데이터를 정렬한다.

2. 피봇을 중심으로, 두 부분으로 나눈다.

3. 그러면, [0,pivot-1] 과 [pivot+1,8]까지의 두 부분으로 나눈 범위를 다시 정렬을 한다.

4. 각 범위의 정렬은 다시 1의 과정과 같음을 알 수 있다.

 

 

 

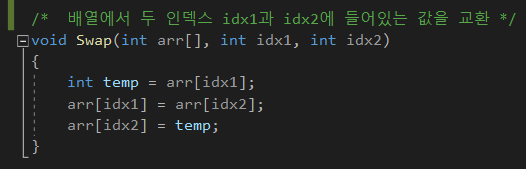
메인 함수

프로그램 실행 결과

 

아래는 소스 파일

main.c

0.00MB