경찰차

1. 문제

어떤 도시의 중심가는 n개의 동서방향 도로와 n개의 남북방향 도로로 구성되어 있다.

 

모든 도로에는 도로 번호가 있으며,  남북방향 도로는 왼쪽부터 1에서 시작하여

n까지 번호가 할당되어 있고 동서방향 도로는 위부터 1에서 시작하여

n까지 번호가 할당되어 있다.

또한, 동서방향 도로 사이의 거리와 남북방향 도로 사이의 거리는 모두 1이다.

 

동서방향 도로와 남북방향 도로가 교차하는 교차로의 위치는 두 도로의 번호의 쌍인

( 동서방향 도로 번호, 남북방향 도로 번호 )로 나타낸다.

n이 6인 경우의 예를 들면 다음과 같다.

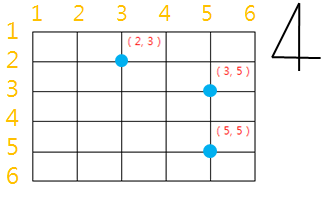
이 도시에는 두 대의 경찰차가 있으며, 두 차를 경찰차1과 경찰차2로 부른다.

처음에는 항상 경찰차1은 (1,1)의 위치에 있고 경찰차2는 (n,n)의 위치에 있다.

 

경찰 본부에서는 처리할 사건이 있으면 그 사건이 발생된 위치를

두 대의 경찰차 중 하나에 알려 주고,

연락 받은 경찰차는 그 위치로 가장 빠른 길을 통해 이동하여 사건을 처리한다.

( 하나의 사건은 한 대의 경찰차가 처리한다. )

 

그리고 사건을 처리한 경찰차는 경찰 본부로부터 다음 연락이 올 때까지,

처리한 사건이 발생한 위치에서 기다린다.

경찰 본부에서는 사건이 발생한 순서대로 두 대의 경찰차에 맡기려고 한다.

 

처리해야 될 사건들은 항상 교차로에서 발생하며 경찰 본부에서는 이러한 사건들을 나누어

두 대의 경찰차에 맡기되, 두 대의 경찰차들이 이동하는 거리의 합을 최소화 하도록 사건을

맡기려고 한다.

 

예를 들어, 위의 그림처럼 n = 6인 경우, 처리해야 하는 사건들이 3개 있고,

그 사건들이 발생된 위치를 순서대로 (3,5), (5,5), (2,3) 이라고 하자.

 

(3,5)의 사건을 경찰차2에 맡기고 (5,5)의 사건도 경찰차2에 맡기며,

(2,3)의 사건을 경찰차1에 맡기면 두 차가 이동한 거리의 합은 4 + 2 + 3 = 9가 되고,

더 이상 줄일 수는 없다.

 

처리해야 할 사건들이 순서대로 주어질 때,

두 대의 경찰차가 이동하는 거리의 합을 최소화 하는 프로그램을 작성하시오.

 

입력

입력 파일의 첫째 줄에는 동서방향 도로의 개수를 나타내는 정수 n

( 3 <= n <= 1,000 )이 주어진다.

둘째 줄에는 처리해야 하는 사건의 개수를 나타내는 정수 w ( 1<= w <= 15 )가 주어진다.

셋째 줄부터 ( w + 2 )번째 줄까지 사건이 발생된 위치가 한 줄에 하나씩 주어진다.

경찰차들은 이 사건들을 주어진 순서대로 처리해야 한다.

각 위치는 동서방향 도로 번호를 나타내는 정수와

남북방향 도로 번호를 나타내는 정수로 주어지며,

두 정수 사이에는 빈 칸이 하나 있다.

두 사건이 발생한 위치가 같을 수 있다.

 

출력

첫째 줄에 두 경찰차가 이동한 총 거리를 출력한다.

2. 문제 분석

이 문제에서 약간의 발상의 전환이 필요하다.

n = 6 일때의 경우를 생각해보자.

두 경찰차의 위치와 3개의 사건의 좌표를 다시 적어보자.

 

경찰차1   ( 1, 1 )

경찰차2   ( 6, 6 )

1번 사건 ( 3, 5 )

2번 사건 ​( 5, 5 )

3번 사건 ( 2, 3 )

​

경찰차1과 1번 사건과의 거리는 다음과 같이 구한다.

abs는 절대값 함수라고 하고 dis가 거리이면

dis = abs(경찰차1의 x좌표 - 1번사건의 x좌표) + abs(경찰차1의 y좌표 - 1번사건의 y좌표)

이와 같은 거리 계산법을 맨하튼 거리 계산이라한다.

 

위의 좌표값을 가지고 하나의 2차원배열을 만들어볼 수 있다.

[그림 1]

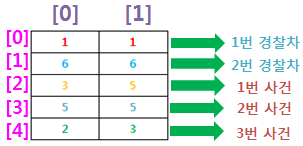
위의 이차원 배열을 통해서 1번 경찰차의 위치를 알고 싶다면,

배열 [0][0] = 1번 경찰차의 x좌표.

배열 [0][1] = 1번 경찰차의 y좌표.​

 

위의 2차원 배열 안에 있는 값들은 각 각 x좌표 y좌표라고 생각하면 된다.

 

두 경찰차와 사건 3개에 대해서 탐색 방법 가지 수는 2^3 인 8가지가 된다.

1. 1번 경찰차가 사건1,사건2,사건3을 모두 차례로 처리하는 경우

2. 1번 경찰차가 사건1과 2를 처리하고 2번 경찰차가 사건 3을 처리

3. 1번 경찰차가 사건1을 처리하고 2번 경찰차가 사건2를 처리하고 1번 경찰차가 사건3을 처리

4. 1번 경찰차가 사건1을 처리하고 2번 경찰차가 사건2를 처리하고 사건3을 처리

5. 2번 경찰차가 사건1을 처리하고 1번 경찰차가 사건2를 처리하고 사건3을 처리

6. 2번 경찰차가 사건1을 처리하고 1번 경찰차가 사건2를 처리하고 2번 경찰차가 사건3을 처리

7. 2번 경찰차가 사건1을 처리하고 2번 경찰차가 사건2를 처리하고 1번 경찰차가 사건3을 처리

8. 2번 경찰차가 사건1,사건2,사건3을 모두 차례로 처리하는 경우

 

그리고 문제에서 나타난 바와 같이 1번 경찰차의 위치가 (1,1)의 위치에 있다고 하고

사건1을 처리했다면 1번 경찰차의 현재 위치는 1번 사건의 위치인 (3,5)이다.

1번 경찰차가 다음 사건을 처리하러 가기위해서 현재의 위치는 (3,5)에서 시작한다.

즉, 각 경찰차들은 사건을 처리하고 그 사건의 위치에서 탐색을 시작한다.

 

이와 같은 탐색을 할 함수의 이름을 Solve라고 한다.

함수의 매개변수는 총 3개가 필요함을 알 수 있다. 두 경찰차들의 위치와 이동한 누적 거리이다.

여기서 경찰차의 위치는 [그림 1]의 이차원 배열의 행의 인덱스로 쓸 것이다.

즉, 1번 경찰차의 초기 위치는 0, 2번 경찰차의 초기 위치는 1이 됨을 알 수 있고

1번 사건 2번 사건 3번 사건의 위치는 각 각 2,3,4 임을 알 수 있다.

위의 [그림 1]의 정보를 저장할 이차원 배열을 아래와 같이 전역 변수로 두고 각 경찰차의 위치와

사건들을 초기화 하도록 하자.

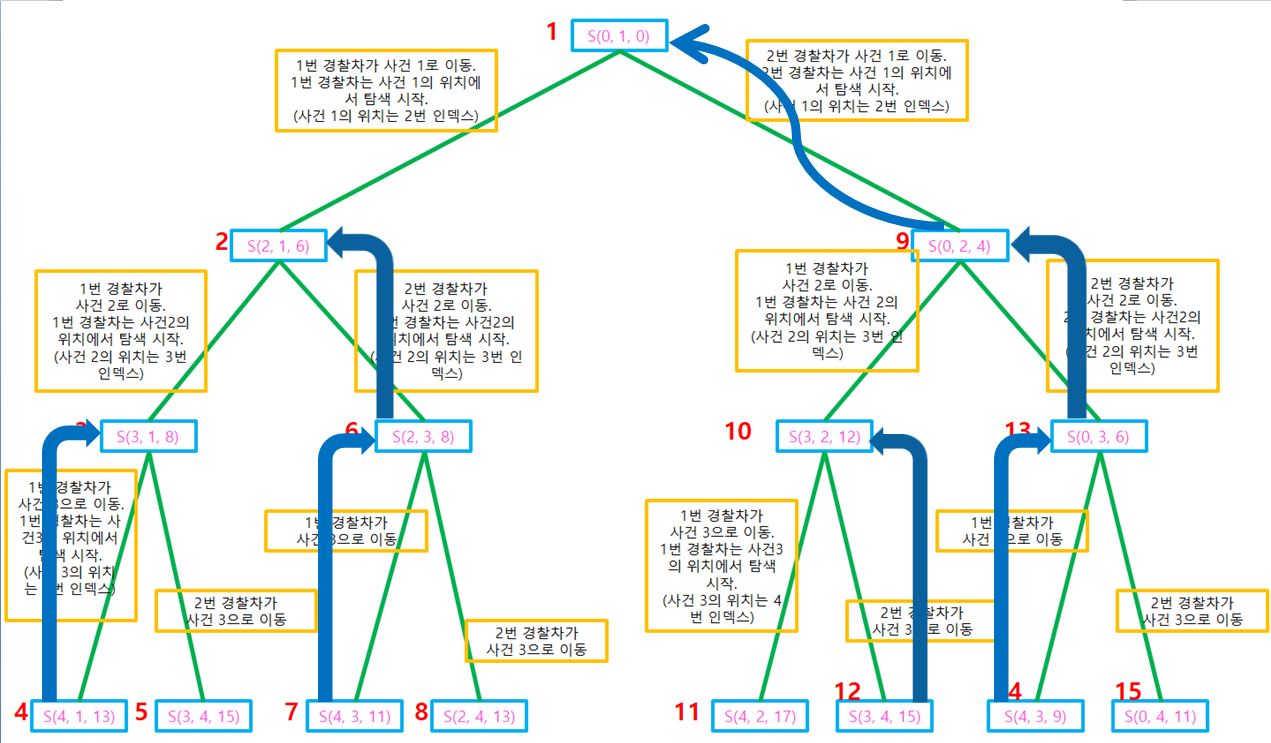
탐색하는 함수는 재귀함수로 구현을 할 것인데, 호출 스택은 아래와 같다.

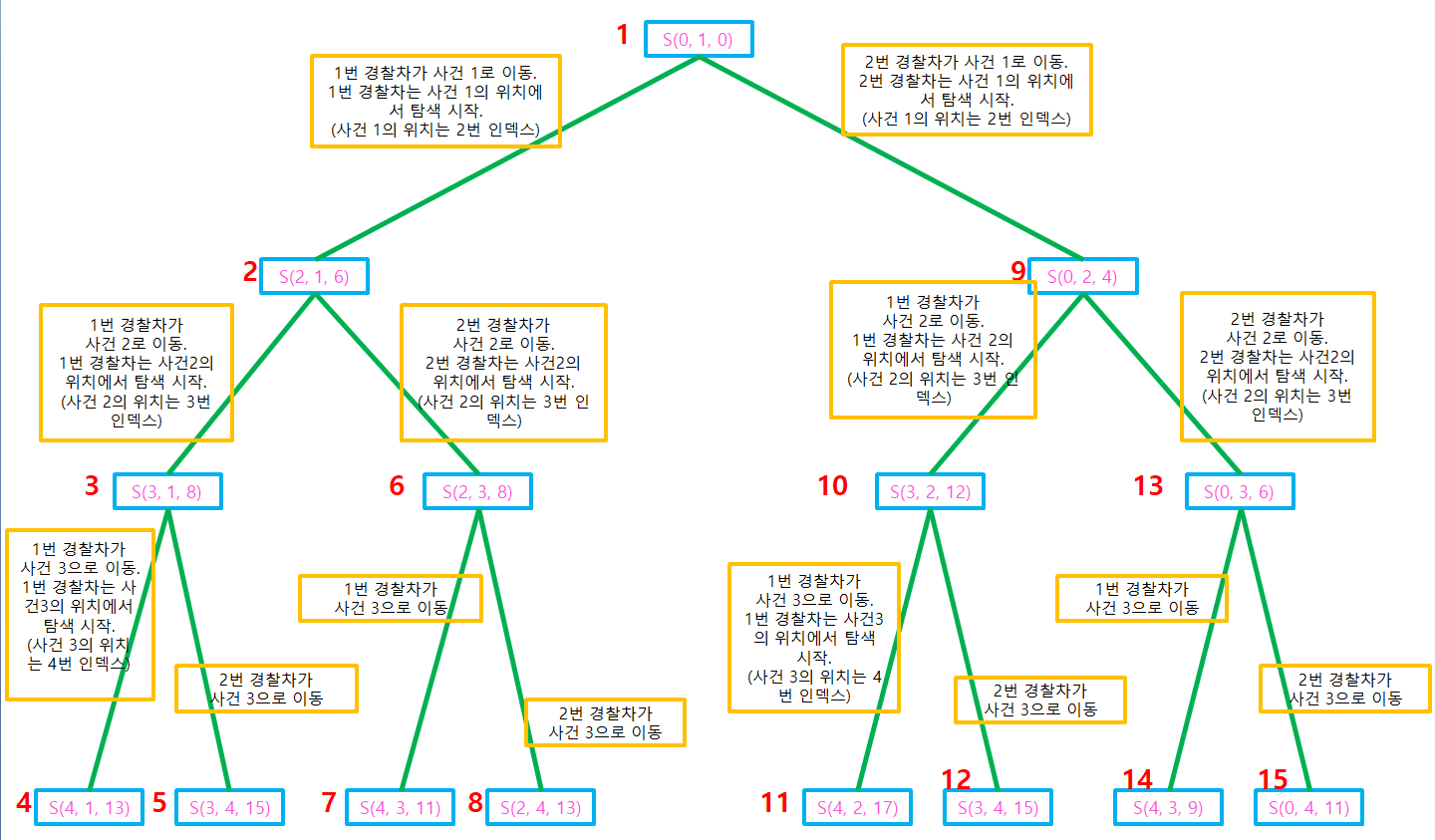
위에서 각 경찰차들이 사건을 해결하면 사건을 해결한 위치에서 탐색을 하는 것을 알 수 있다.

위의 내용을 토대로 탐색하는 함수는 아래와 같다.

3. 구현

프로그램 실행결과

4. 소스 파일

main.c

0.00MB

5. 연산량을 좀 더 줄일 수 있는 방법

프로그램 실행결과

6. 소스 파일

main.c

0.00MB

 

7. 다른 방법의 풀이

이진 탐색 트리에서 트리의 높이를 구하는 방식과 비슷한 방법으로 구할 수 있다.

즉, 여기서는 두 경찰차가 모든 사건을 처리하고 난 이후의 움직인 거리들 중에서 최소 거리를 반환하는 방식이다. 

 

프로그램 실행결과

8. 소스 파일

main.c

0.00MB

 

9. 위의 내용을 동적 프로그래밍을 이용해 구현

프로그램 실행결과

소스 파일

main.c

0.00MB