점과 점의 각도(삼각함수의 역함수를 이용)

1. 설명

 

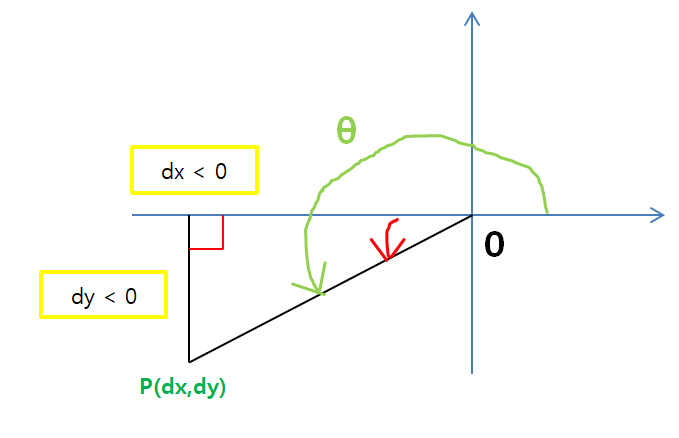
위의 정보를 가지고 우리는 각도 theta를 구할 수 있다.

dx와 dy를 알고 있으므로 이는 tangent함수를 이용해서 구할 수 있다.

각도는 반시계 방향을 기준으로 한다.

 

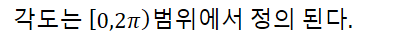
위의 내용으로부터 알 수 있는 사실은 dx와 dy만 구하면, 두 점에서의 각을 구할 수 있다.

 

case1. originPos와 destPos의 x좌표와 y좌표가 모두 일치하는 경우

dx = 0, dy = 0 

 

case2. originPos의 y좌표와 destPos의 y좌표가 일치하는 경우

(1). dy = 0, dx > 0

(2). dy = 0, dx < 0

case3. originPos의 x좌표와 destPos의 x좌표가 일치하는 경우

(1). dx = 0, dy > 0

(2). dx = 0, dy < 0

case4. 나머지의 경우

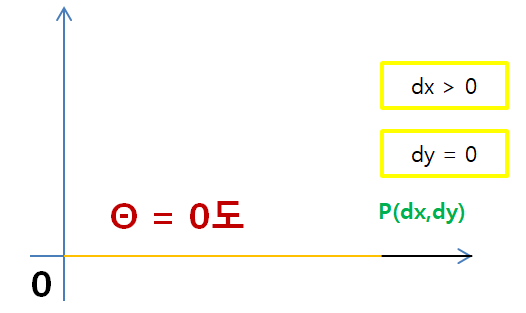
(1). dx > 0 and dy > 0 이면 1사분면

tangent함수는 1사분면에서 양수값을 갖는다.

atan(dy/dx) 가 theta값이다.

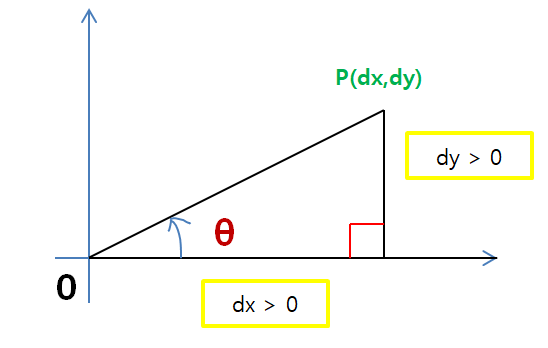
(2). dx > 0 and dy < 0 이면 4사분면

tangent함수는 4사분면에서 음수값을 갖는다.

atan(dy/dx) + 360를 하면 theta값을 구할 수 있다.

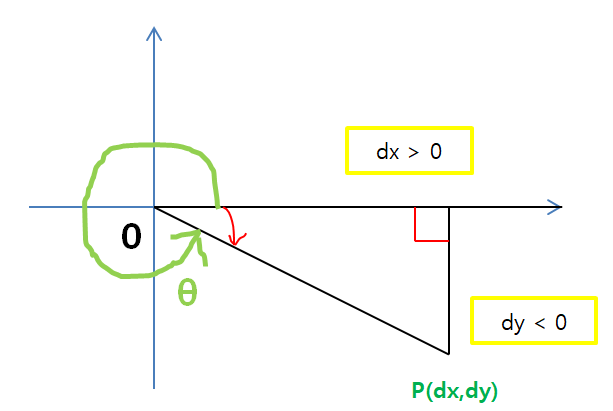
(3). dx < 0 and dy > 0 이면 2사분면

tangent함수는 2사분면에서 음수값을 갖는다.

atan(dy/dx) + 180를 하면 theta값을 구할 수 있다.

(4). dx < 0 and dy < 0 이면 3사분면

tangent함수는 3사분면에서 양수값을 갖는다.

atan(dy/dx) + 180를 하면 theta값을 구할 수 있다.

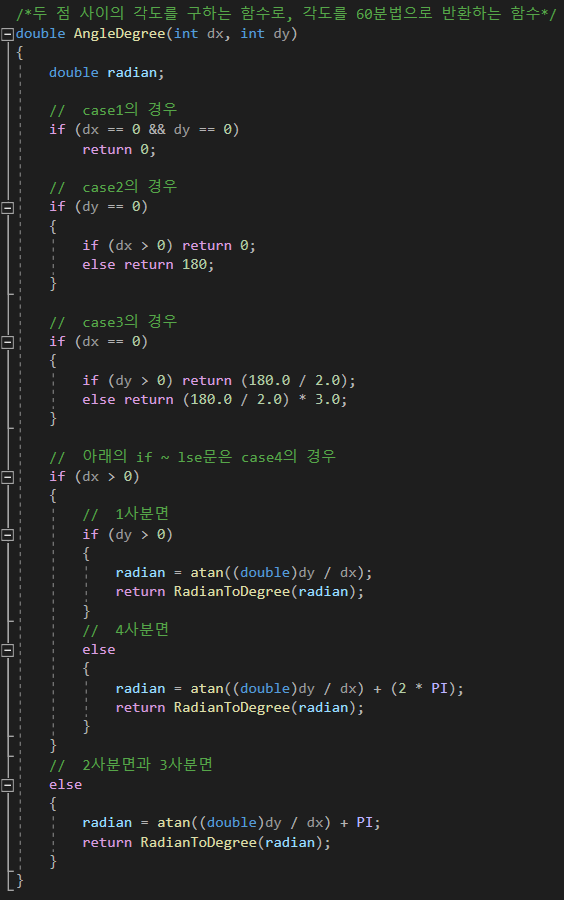
2. 두 점 사이의 각도를 구하는 함수

각도를 구하기 위해서는 atan함수를 이용하면 되는데, 이 함수의 리턴값은 호도법이다.

즉, 우리가 눈으로 보기에는 호도법 보다는 60분법으로 보는 것이 더 직관적이다.

이에 따라 두 점 사이의 각도를 구하는 함수는 두 개로 만들어보자.

하나는 호도법으로 리턴을 하고 다른 하나는 각도로 리턴을 하도록 하자.

위의 내용을 토대로 함수를 만들면 다음과 같다.

3. 구현

프로그램 실행결과1

프로그램 실행결과2

originPos는 그대로 두고, destPos를 {3,1}로 두면

프로그램 실행결과3

originPos는 그대로 두고, destPos를 {-3,1}로 두면

프로그램 실행결과4

originPos는 그대로 두고, destPos를 {1,-4}로 두면

프로그램 실행결과5

originPos는 그대로 두고, destPos를 {1,1}로 두면

프로그램 실행결과6

originPos는 그대로 두고, destPos를 {2,2}로 두면

프로그램 실행결과7

originPos는 그대로 두고, destPos를 {-1,3}로 두면

프로그램 실행결과8

originPos는 그대로 두고, destPos를 {-1,-1}로 두면

프로그램 실행결과9

originPos는 그대로 두고, destPos를 {3,-1}로 두면

4. 소스 파일

main.c

0.00MB